This paper describes the emulation of a triode amplifier stage of the type typically found at the front end of a guitar amplifier. The emulation includes predominantly second order non-linearity, clipping at the input due to grid current and clipping at the output due to cutoff. The non linear element is a bipolar transistor.
Why Use A BJT? - The Problem With JFETs
While there seem to be several reasonably convincing triode emulators using jfets, they all suffer from the basic jfet problem which is the extreme variability of their main parameters. This can be factored out to some extent when the jfets are used as part of a linear amplifier but is a serious obstacle when it comes to designing a reproducible non-linear circuit. The variations can cover a five to one range, necessitating selection of components or the provision of trimming. Even after trimming there remains a variation in gain or clipping level.
Bipolar transistors, on the other hand, are extremely predictable and well behaved. The non-linearity of the transfer function gm, or ∆ic/∆vbe, although varying with temperature, is well defined.
First, some well known results:
Typically, at a room temperature of 18C and for a bias current of 1mA, considering variations about the bias point and nomalising we have
ic = exp(40*v) - 1
This can be expanded as a power series in v:
ic = 40.0*v + 800.0*v^2 + 10666*v^3 + 1.06667e+5*v4 + 8.53333e+5*v^5 + ...
At first glance this seems to be hopelessly non-linear, but if we confine v to small values such as 10mV, the picture is somewhat more benign, as might be expected of a power series.
ic(v=10mv)=400m + 80m(v^2 term) + 10m7(v^3 term) + 1m07(v^4 term) + 85u(v^5 term)
At lower levels, the second order term dominates even more. In fact, it is a well known result that the distortion of a voltage driven transistor stage is mostly second harmonic and is proportional to the peak input voltage, being 1% at 1mV, 10% at 10mV.
It may seem strange at first to be modelling a triode with an essentially square law non-linearity approximated by an exponential rather than seeking to achieve the 3/2 power of Child's law but there are two reasons why this approach is valid:
- Many triodes (including the ECC83) actually follow a square law rather than a 3/2 law. Using data from the ECC83 datasheet, try plotting anode current against anode voltage squared at a fixed grid voltage.
- We are emulating the behaviour, not the underlying physics, so there is no need to consider operation outside our region of interest. The basic biasing of the stage, for example, is taken care of separately from the modelling of the dynamics.
So, we have our basic non-linear element, although it only works at millivolt levels.
Further considerations:
The dynamic output resistance of the transistor is high; its behaviour is often compared to that of a pentode. The triode, on the other hand, has a relatively low output resistance caused by the internal feeback where both the grid and the anode influence the electric field at the grid. The feedback factor is 1/µ and our emulator must include this.
Next, the triode doesn't follow the same non-linear law all the way down to cutoff. It smoothly enters a quasi-exponential region where the gain tails off.
Finally, the input resistance of the triode falls rapidly when the grid voltage is brought above that of the cathode and the grid current rises.
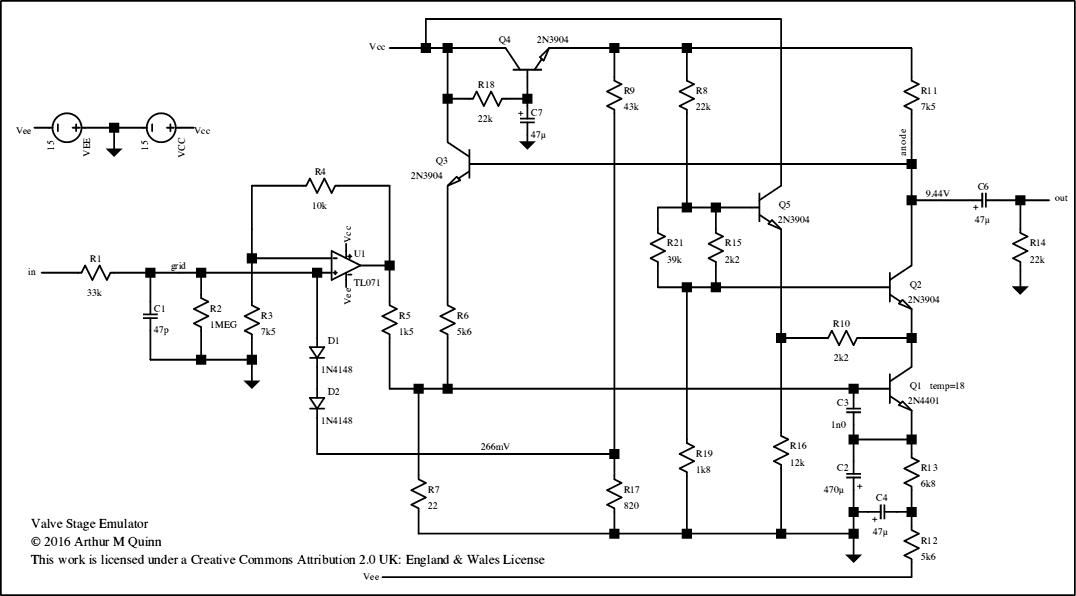
The version of the circuit shown above requires reasonably stable power supplies of +/-15V. There are many miniature switchmode modules that can provide these, even from a battery supply.
Because of the choice of such a low anode voltage compared to a real triode stage and the need to keep the input clipping range comparable to that of a triode, the overall gain is limited, in this case to 12dB. The use of high voltage transistors such as type KSP44 for the cascode and feedback would allow the use of a higher anode voltage (150V or so) which could give a gain and output swing directly comparable to an ECC83 stage.
The main gain and non-linear transistor is Q1 which is biased to about 1.1mA via R12 and R13. The emitter of Q1 is decoupled to ground by C2, which has to have such a high value to decouple the low effective emitter resistance of about 23Ω. The output current of Q1 passes to the anode load, R11, via Q2 in a cascode configuration. Current through R10 is subtracted from that coming from Q1 so that Q2 will clip a predetermined amount before Q1, emulating the change in behaviour of the triode towards cutoff. The slope of the clipping curve is reduced by the relatively low value of R10. Q5, biased by R15/R21, provides a reference voltage above the emitter voltage of Q2 to define the quiescent current through R10. In the quiescent state, the emitter currents of Q1 and Q5 are approximately equal to minimise any temperature drift of the voltage across R10. The voltage across R19, just under 1V provides the base reference for cascode transistor Q2. This results in Q1 being operated with a very low collector voltage and maximises the possible output voltage swing. The whole emulator contains only one time constant, that of C2 and re of Q1. This is analogous to the cathode decoupling of the valve.
The input diode pair representing the grid - cathode diode is biased by a separate potential divider R9/R17
The input to Q1 is developed across R7 which is chosen to be of a low value to minimise noise. Feedback is via R6, buffered by Q3.
In an ideal world, one would use a transformer to match the required high input impedance of the valve to the small resistor needed for noise control. In practice, op amp U1 is used as a buffer to feed the feedback summing point via R5
D1 and D2, reversed biased by the voltage across R17, provide grid current when the input is overdriven.
Q5 with R18 and C7 provides decoupling of any noise on the positive power rail. The voltage drop across Q5 also provides headroom for Q3 when the output voltage rises to the rail.
Distortion and clipping
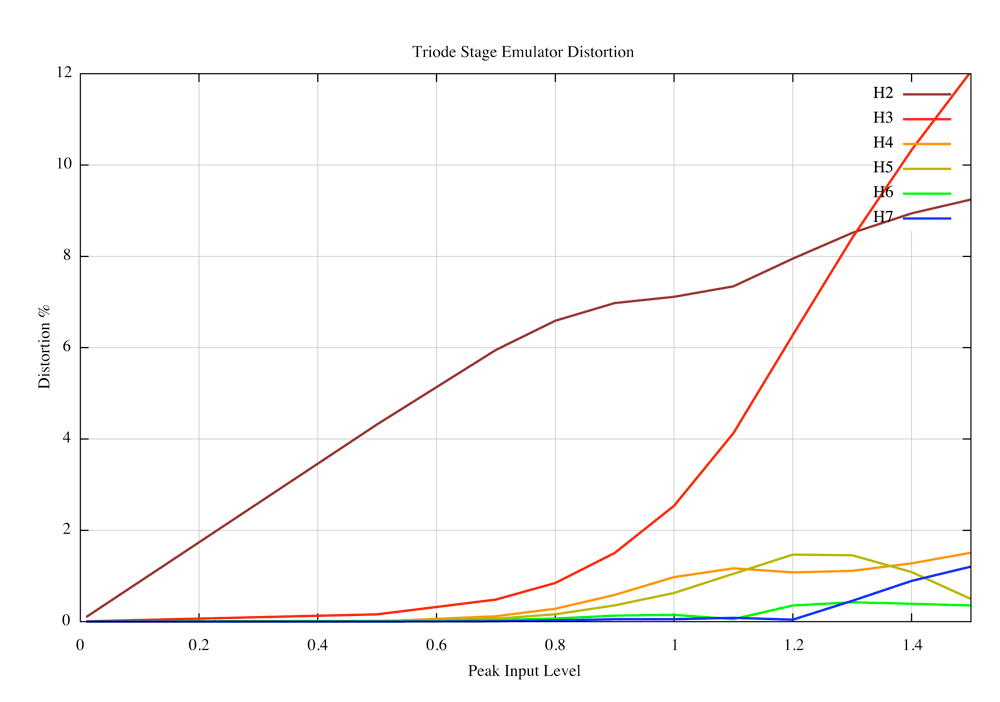
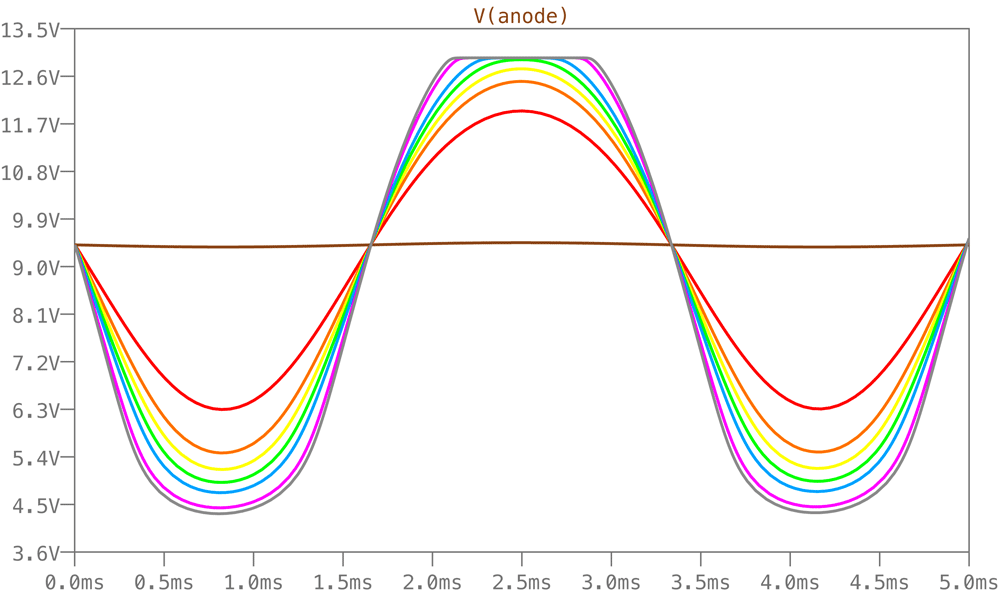
The circuit as it stands clips by cutoff for negative excursions of the input and by grid current for positive excursions, Distortion just before clippng is about six percent, which is on the high side of ECC83 performance. Juggling the feedback, the anode load and the current subtracted at Q2 emitter via R10 allows variation either way.
Noise
A major difficulty when attenuating the signal to the 10 - 15mV required to drive Q1 is achieving adequate noise performance. Q1 is a medium power transistor known for its low extrinsic base resistance and hence good noise performance at low impedance levels. The source resistance for Q1 is kept low at 22Ω, roughtly equal to the emitter resistance. The extra signal power required to do this comes from op amp U1. The main sources of noise are Q1, R22, R1 and U1. The noise contributions of the other transistors are negligible and any general purpose type of reasonable gain will do. The A-Weighted noise at the output is 14µ8V, corresponding to 4µ7V at the input. This is 5dB higher than an equivalent ECC83 stage including the input buffering resistor R1 but is, of course, free from any hum. The A-Weighted signal to noise ratio would be over 76dB for a 30mV input. As can be seen from the above graph, input clipping occurs at about 1.4V peak or 1V rms, at which point the signal to noise ratio would be 106 dB
Output resistance, µ and gm
The gm of Q1 is 44mS. The effective µ of the stage is 3k3/22 = 150. The anode resistance is, therefore, ra = µ/gm = 3k4Ω. This is much lower than that of a conventional small signal triode but is in proportion to the 7k5Ω anode load. Note that gm is a measure of variation and is not affected by subtracting a fixed current at Q2 emitter.
In a high voltage version of the circuit, gm would be maintained at the same value, since it is a function of Q1 emitter current and is very much constrained by noise considerations. The value of R6 would be increased, raising µ and hence the anode resistance. The anode load, R11, would increase necessitating a much reduced base current through Q3, which might then need to be a Darlington pair.
Miller Capacitance
The circuit as drawn does not include any capacitance between anode and grid. Instead, C1 is included to provide some high frequency filtering. If desired, a capacitor can be connected between the anode and the input. In order to achieve the same effect as the 2pF Cag of an ECC83, say, it would have to be roughly ten times larger to account for the lower overall gain. This capacitance, when viewed from the grid, would appear to be non-linear. Whether this is an effect worth reproducing is unknown.
© 2016 Arthur M Quinn

This work is licensed under a Creative
Commons Attribution 2.0 UK: England & Wales License.